

If told to find all values of a cricle given a radius of length 7, you can use the calculation process. If given the radius then the diameter is already two times that value and if given the diameter, the radius is half of that value. Since the triangle's three sides are all tangents to the inscribed circle, the distances from the circle's center to the three sides are all equal to the circle's radius. Finding values in a circle is very simple because only one value in a circle is needed to find all other values.
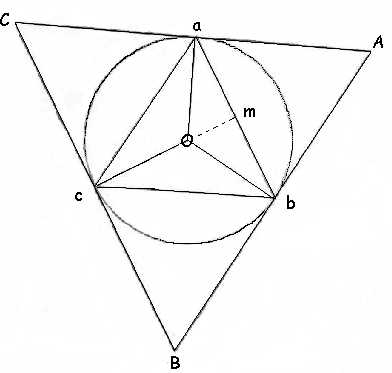
In this situation, the circle is called an inscribed circle, and its center is called the inner center, or incenter. In this situation, the circle is called an inscribed circle, and its center is called the inner center, or incenter. A circle is inscribed in the triangle if the triangle's three sides are all tangents to a circle. The circle that is tangent to each side of the triangle is the. Draw a line segment (called the 'altitude') at right angles to a side that goes to the opposite corner. Here are some posts on circles and polygons inscribed in them.A circle is inscribed in the triangle if the triangle's three sides are all tangents to a circle. With the topics seen in this lesson, the challenge presented at the beginning can be answered. R is given directly so you can get the area of the triangle. When do you observe point J to be inside or outside the triangle. These angle bisectors meets at three points outside the triangle ABC. Some outer edges of the picture may be cropped away. Use this centre and OA as radius, we can draw a circle passing through the. You can get r from here and subsequently the area of the triangle The applet below shows a circle circumscribed about triangle ABC with circumcenter at. Crop an image to a shape, such as a circle Fill Fills the entire shape with the picture. Express the area within the circle but outside the triangle as a. This article discusses the three types of angles that have their vertex outside a circle: secant-secant angles, secant-tangent angles, and tangent-tangent angles. An isosceles triangle is inscribed in a circle of radius R, where R is a constant. When an equilateral triangle is inscribed in a circle, Side of the triangle = √3 * Radius of the circleĪrea of triangle \(= \sqrtr^2/4 = 3*pi\) An angle that intersects a circle can have its vertex inside, on, or outside the circle. (2) alone is sufficient.Īlso note that we can answer DS questions without actually solving the question, we just need to prove if the data given in 1/2 are sufficient or not. These geometrical shapes could be a circle, a square, a triangle.

If (2) using r we can calculate the area of triangle since we know length of each side and height in terms of r. The outer figure touches the maximum points of the inside figure without crossing it. If (1) is known r can be calculated, since the area outside the triangle is difference of two figures that can be written in terms of r and subsequently we can calculate the area of the triangle. Given this, the area of triangle can be written in terms of r and also we know area of circle in terms of r that is pi*r^2 - so we should assess each option if it is sufficient to identify what r is Using the b h 2 formula for a triangle area gives that the requested area of O A P is. Length and height of each side of the triangle can be written in terms of r using the Isosceles Triangle from the center of the circle to any two corners of triangle (angles: 120, 30 30) To get the location where this line crosses the x -axis, set y 0 in the equation above to get. What is the área of an equilateral triangle inscribed in a circle?


 0 kommentar(er)
0 kommentar(er)
